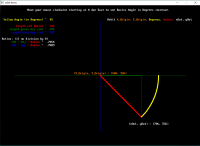
Orbit sub calculates points about a point cx, cy at a given angle in degrees and radius using trig functions COS and SIN ratios according to degrees.
edit: to show when sin and cos go negative. abs() should only be applied to lengths.
Notice 0 Degrees is due East and as the angle in degrees increases the the arc goes CLOCK-WISE about cx, cy from EAST to SOUTH to WEST to NORTH and returns to due EAST at 360 degrees, one complete turn.
Code: (Select All)
Option _Explicit
_Title "orbit demo" 'b+ 2024-05-10
'============================== Main
Const Xmax = 1000, Ymax = 700
Const Thick = 2
Const Arc_Radius = 100
Const Sin_color = _RGB32(0, 0, 255)
Const Cos_color = _RGB32(0, 128, 0)
Const Radius_color = _RGB32(255, 0, 0)
Const Ang_color = _RGB32(255, 255, 0)
Const White = _RGB32(255, 255, 255)
Const Origin_color = _RGB32(255, 128, 0)
Dim cx, cy, mx, my, stepX, stepY, Radius, dAng, xOut, yOut, x, y
cx = Xmax / 2: cy = Ymax / 2
Screen _NewImage(Xmax, Ymax, 32)
_ScreenMove 60, 0
_PrintMode _KeepBackground
_MouseMove cx + 100, cy + 100 ' get ball rolling
While 1
Cls
Color White
Locate 2, 18
Print "Move your mouse clockwise starting at 0 due East to see Basics Angle in Degrees increase."
Locate 5, 68
Print "Orbit ";
Color Origin_color
Print "X_Origin, Y_Origin,";
Color Ang_color
Print " Degrees,";
Color Radius_color
Print " Radius,";
Color White
Print " xOut, yOut"
'draw horizontal through center of screen
Line (70, cy)-(Xmax - 70, cy), Cos_color
' draw vertical line through center of screen
Line (cx, 70)-(cx, Ymax - 70), Sin_color
'poll mouse
While _MouseInput: Wend ' updates all mouse stuff except wheel
mx = _MouseX: my = _MouseY 'get mouse location
'draw our Color Coded Trig Triangle
ThickLine cx, cy, mx, cy, 1, Cos_color
ThickLine mx, cy, mx, my, 1, Sin_color
ThickLine cx, cy, mx, my, Thick, Radius_color
stepX = mx - cx: stepY = my - cy
Radius = (stepX ^ 2 + stepY ^ 2) ^ .5
'to draw angle need to do some math
'dAng = mouse angle to 0 Degrees due East
dAng = _R2D(_Atan2(my - cy, mx - cx))
If dAng < 0 Then dAng = dAng + 360
Color Ang_color
ThickArc cx, cy, Radius, 0, dAng, Thick
'report all numbers color coded
Color Ang_color
Locate 5, 3: Print "Yellow Angle (in Degrees) ~ "; dAng \ 1
Color Radius_color
Locate 7, 7: Print " Length red Radius ~ "; Radius \ 1
Color Sin_color
Locate 9, 7: Print " Length blue Opp side ~ "; Abs(stepY) \ 1
Color Cos_color
Locate 8, 7: Print "Length green Adj side ~ "; Abs(stepX) \ 1
Color White
Locate 11, 1: Print " Ratios: (if no division by 0)"
If Radius <> 0 Then
Color Cos_color
Locate 12, 8: Print "COS = Adj ";
Color Radius_color
Print "/ Radius ";
Color White
Print "~ "; Left$(Str$(stepX / Radius), 6) '; Cos(_D2R(dAng)) ' double check
Color Sin_color
Locate 13, 8: Print "SIN = Opp ";
Color Radius_color
Print "/ Radius ";
Color White
Print "~ "; Left$(Str$(stepY / Radius), 6) '; Sin(_D2R(dAng)) ' double check
End If
Color White
orbit cx, cy, dAng, Radius, xOut, yOut ' mouse here
orbit cx, cy, dAng, Radius + 50, x, y ' set label here
label x, y, "(xOut, yOut) = (" + _Trim$(Str$(xOut \ 1)) + "," + Str$(yOut \ 1) + ")"
Color Origin_color
label cx, cy - 10, "(X_Origin, Y_Origin) = (" + _Trim$(Str$(cx)) + "," + Str$(cy) + ")"
_Display
_Limit 60
Wend
' !!!!!! featuring the use of this SUB routine !!!!
Sub orbit (X_Origin, Y_Origin, Degrees, Radius, xOut, yOut) ' all default single should be ok
xOut = X_Origin + Radius * Cos(_D2R(Degrees))
yOut = Y_Origin + Radius * Sin(_D2R(Degrees))
End Sub
Sub label (xc, yc, text$)
Dim th2, pw2
th2 = _FontHeight / 2
pw2 = _PrintWidth(text$) / 2
_PrintString (xc - pw2 + 1.25, yc - th2 + .5), text$
End Sub
Sub ThickArc (xCenter, yCenter, arcRadius, dAngleStart, dAngleEnd, rThick)
Dim rAngle, rAngleStart, rAngleEnd, x1, y1, Stepper
'draws an Arc with center at xCenter, yCenter, Radius from center is arcRadius
'for SmallBASIC angle 0 Degrees is due East and angle increases clockwise towards South
'THIS SUB IS SETUP TO DRAW AN ARC IN CLOCKWISE DIRECTION
'dAngleStart is where to start Angle in Degrees
' so make the dAngleStart the first ray clockwise from 0 Degrees that starts angle drawing clockwise
'dAngleEnd is where the arc ends going clockwise with positive Degrees
' so if the arc end goes past 0 Degrees clockwise from dAngleStart
' express the end angle as 360 + angle
'rThick is the Radius of the many,many tiny circles this will draw to make the arc thick
' so if rThick = 2 the circles will have a Radius of 2 pixels and arc will be 4 pixels thick
If arcRadius < 1 Then PSet (xCenter, yCenter): Exit Sub
rAngleStart = _D2R(dAngleStart): rAngleEnd = _D2R(dAngleEnd)
If Int(rThick) = 0 Then Stepper = 1 / (arcRadius * _Pi) Else Stepper = rThick / (arcRadius * _Pi / 2)
For rAngle = rAngleStart To rAngleEnd Step Stepper
x1 = arcRadius * Cos(rAngle): y1 = arcRadius * Sin(rAngle)
If Int(rThick) < 1 Then
PSet (xCenter + x1, yCenter + y1)
Else
fcirc xCenter + x1, yCenter + y1, rThick, Ang_color
End If
Next
End Sub
Sub ThickLine (x1, y1, x2, y2, rThick, K As _Unsigned Long)
Dim length, stepx, stepy, dx, dy, i
'x1,y1 is one endpoint of line
'x2,y2 is the other endpoint of the line
'rThick is the Radius of the tiny circles that will be drawn
' from one end point to the other to create the thick line
'Yes, the line will then extend beyond the endpoints with circular ends.
stepx = x2 - x1
stepy = y2 - y1
length = (stepx ^ 2 + stepy ^ 2) ^ .5
If length Then
dx = stepx / length: dy = stepy / length
For i = 0 To length
fcirc x1 + dx * i, y1 + dy * i, rThick, K
Next
End If
End Sub
Sub fcirc (CX As Long, CY As Long, R As Long, C As _Unsigned Long)
Dim Radius As Long, RadiusError As Long
Dim X As Long, Y As Long
Radius = Abs(R): RadiusError = -Radius: X = Radius: Y = 0
If Radius = 0 Then PSet (CX, CY), C: Exit Sub
Line (CX - X, CY)-(CX + X, CY), C, BF
While X > Y
RadiusError = RadiusError + Y * 2 + 1
If RadiusError >= 0 Then
If X <> Y + 1 Then
Line (CX - Y, CY - X)-(CX + Y, CY - X), C, BF
Line (CX - Y, CY + X)-(CX + Y, CY + X), C, BF
End If
X = X - 1
RadiusError = RadiusError - X * 2
End If
Y = Y + 1
Line (CX - X, CY - Y)-(CX + X, CY - Y), C, BF
Line (CX - X, CY + Y)-(CX + X, CY + Y), C, BF
Wend
End SubNotice 0 Degrees is due East and as the angle in degrees increases the the arc goes CLOCK-WISE about cx, cy from EAST to SOUTH to WEST to NORTH and returns to due EAST at 360 degrees, one complete turn.
724 855 599 923 575 468 400 206 147 564 878 823 652 556 bxor cross forever




