Draw that Circle

[James D Jarvis]

I was playing with alternate means draw filled circles and had the most success with the following routine.

the basic algorithm is simple:  determine the center of the circle , plot the y axis out to the distance or R (negative to positive) and calculate X for each Y. Draw a line at X across the Y axis for each point of Y until there's a circle.

I was playing with a number of different methods to draw and do the calculations and the ones included here are good to share.

rcircle took  .8789062 to .9335938 seconds
dcircle took .6015625 to .6601562 seconds
dmcircle took .6015625 to .6601562 seconds

dcircle tended to get the best draw time on my computer, it had the same  range as dmcircle but it tended to be lower on average so certainly a win for the reference table but no clear advantage to using mem to access the look up table.

EDIT: typo corrected... better version of the rcircle sub is later in the thread

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer
Print "that was"; t6 - t5; " seconds for 64,000 circles"
Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"

_MemFree nsq

Sub rcircle (cx, cy, r, klr)
'simple filled circle drawing with making use of paint command
    For y = -r To r
        x = Sqr(r ^ 2 - y ^ 2)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        ' Print x
    Next y
End Sub

Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub

[bplus]

rcircle is now the leader of the pack:

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer
Print "that was"; t6 - t5; " seconds for 64,000 circles"
Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"

_MemFree nsq


Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub


Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
 
    rsqrd = r * r
    For y = 0 To r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        ' Print x
    Next
End Sub

[bplus]

Even better:

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer
Print "that was"; t6 - t5; " seconds for 64,000 circles"
Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"

_MemFree nsq


Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub


Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

[SMcNeill]

I see your times and I ... umm...  slightly improve upon them with two magic letters...

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer

Print "that was"; t6 - t5; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
t7 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
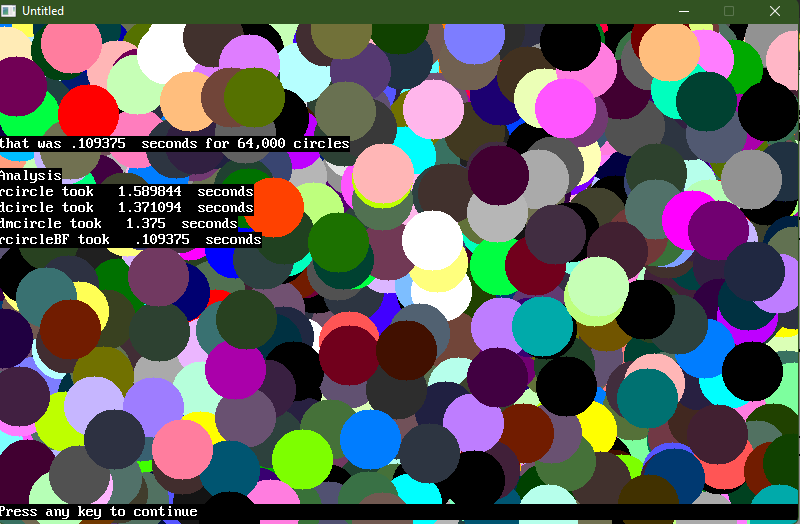
    rcircleBF Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t8 = Timer
Print "that was"; t8 - t7; " seconds for 64,000 circles"


Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"
Print "rcircleBF took  "; t8 - t7; " seconds"

_MemFree nsq


Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub


Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

Sub rcircleBF (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr, BF
        Line (cx - x, cy - y)-(cx + x, cy - y), klr, BF
        y = y + 1
    Wend
End Sub

   

[James D Jarvis]

Excellent. I had been looking at it too long and totally forgot calculating r^2 only has to happen once.  Thank you.

Code: (Select All)

Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

[bplus]

Oh get rid of overlapping lines you can only catch using Alpha coloring:

Code: (Select All)

Screen _NewImage(800, 620, 32)
Randomize Timer
rcircle 400, 310, 300, _RGB32(200, 250, 40, 20) ' <<< look for overlapping lines using alpha color
Sleep

Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    Dim x, y As Long
    rsqrd = r * r
    Line (cx - r, cy)-(cx + r, cy), klr  ' one line at y = 0
    y = 1
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

[James D Jarvis]

I see your times and I ... umm...  slightly improve upon them with two magic letters...

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer

Print "that was"; t6 - t5; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
t7 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    rcircleBF Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t8 = Timer
Print "that was"; t8 - t7; " seconds for 64,000 circles"


Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"
Print "rcircleBF took  "; t8 - t7; " seconds"

_MemFree nsq


Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub


Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

Sub rcircleBF (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr, BF
        Line (cx - x, cy - y)-(cx + x, cy - y), klr, BF
        y = y + 1
    Wend
End Sub

Doh.    I had been working with direct memory writes with other experimental routines and had stopped trying to copy BF and went on to forget about BF.

[bplus]

Wow BF makes that much a difference? Seems like something is wrong about Line?

[SMcNeill]

And here's one with my standard CircleFill routine to compare speeds with:

Code: (Select All)

'Draw_that_circle
'
'By James D. Jarvis
'
'an alternate subroutine to draw a filled circle.
'the basic sub is rcircle, rcircle find X while stepping through Y for -radius to the radius
'dcircle,  references the precalculated table in the array nsqr() to otherwise drae as rcircle
'dmcircle, references the precalculated table in the array nsqr() as dcircle but makes uses of _mem for access.

Screen _NewImage(800, 500, 256)
Randomize Timer
Dim Shared nsqr(-32000 To 32000) As Long 'table holds the square values
Dim Shared nsq As _MEM 'let's access the memblock of the table

For n = -32000 To 32000 'precaluclaitng the square values of -32000 to 32000
    nsqr(n) = Abs(n) ^ 2
Next
nsq = _Mem(nsqr())
Input "press enter to start"; any$

'draw without look up table
t1 = Timer
For n = 1 To 64000
    ' r = Int(1 + Rnd * 60) 'comment this out in each l0op to see the difference with a fixed radius
    r = 30 'chanign the size certainyl crerates a speed difference
    rcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t2 = Timer
Print "that was"; t2 - t1; " seconds for 64,000 circles"

'draw with look up table
Input "Press enter to continue"; A$
t3 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t4 = Timer
Print "that was"; t4 - t3; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
'draw with look up table and using mem offset
t5 = Timer
For n = 1 To 64000
    'r = Int(1 + Rnd * 60)
    r = 30
    dmcircle Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t6 = Timer

Print "that was"; t6 - t5; " seconds for 64,000 circles"
Input "press enter to continue"; ask$
t7 = Timer
For n = 1 To 640000
    'r = Int(1 + Rnd * 60)
    r = 30
    rcircleBF Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t8 = Timer
Print "that was"; t8 - t7; " seconds for 640,000 circles"
Input "press enter to continue"; ask$
t9 = Timer
For n = 1 To 640000
    'r = Int(1 + Rnd * 60)
    r = 30
    CircleFill Int(Rnd * 800), Int(Rnd * 500), r, Int(Rnd * 256)
Next n
t10 = Timer
Print "that was"; t10 - t9; " seconds for 640,000 circles"


Print
Print "Analysis"
Print "rcircle took  "; t2 - t1; " seconds"
Print "dcircle took  "; t4 - t3; " seconds"
Print "dmcircle took  "; t6 - t5; " seconds"
Print "rcircleBF took  "; t8 - t7; " seconds (for 10x the number of circles)"
Print "CircleFill took  "; t10 - t9; " seconds (for 10x the number of circles)"

_MemFree nsq


Sub dcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub dmcircle (cx, cy, r, klr)
    'simple routine to draw a circle using a look up table to speed up calculations
    y = -r
    Do
        x = Sqr(_MemGet(nsq, nsq.OFFSET + (r + 32000) * 4, Long) - _MemGet(nsq, nsq.OFFSET + (y + 32000) * 4, Long))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Loop Until y > r
End Sub

Sub wcircle (cx, cy, r, klr)
    'was testing if there was a notable difference between using a do loop or a while loop, left it here if anyone else wanted to try it
    y = -r
    While y <= r
        x = Sqr(nsqr(r) - nsqr(y))
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        y = y + 1
    Wend
End Sub


Sub rcircle (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr
        Line (cx - x, cy - y)-(cx + x, cy - y), klr
        y = y + 1
    Wend
End Sub

Sub rcircleBF (cx As Long, cy As Long, r As Long, klr As _Unsigned Long)
    rsqrd = r * r
    y = 0
    While y <= r
        x = Sqr(rsqrd - y * y)
        Line (cx - x, cy + y)-(cx + x, cy + y), klr, BF
        Line (cx - x, cy - y)-(cx + x, cy - y), klr, BF
        y = y + 1
    Wend
End Sub

Sub CircleFill (CX As Long, CY As Long, R As Long, C As Long)
    Dim Radius As Long, RadiusError As Long
    Dim X As Long, Y As Long

    Radius = Abs(R)
    RadiusError = -Radius
    X = Radius
    Y = 0

    If Radius = 0 Then PSet (CX, CY), C: Exit Sub

    ' Draw the middle span here so we don't draw it twice in the main loop,
    ' which would be a problem with blending turned on.
    Line (CX - X, CY)-(CX + X, CY), C, BF

    While X > Y
        RadiusError = RadiusError + Y * 2 + 1
        If RadiusError >= 0 Then
            If X <> Y + 1 Then
                Line (CX - Y, CY - X)-(CX + Y, CY - X), C, BF
                Line (CX - Y, CY + X)-(CX + Y, CY + X), C, BF
            End If
            X = X - 1
            RadiusError = RadiusError - X * 2
        End If
        Y = Y + 1
        Line (CX - X, CY - Y)-(CX + X, CY - Y), C, BF
        Line (CX - X, CY + Y)-(CX + X, CY + Y), C, BF
    Wend

End Sub

   

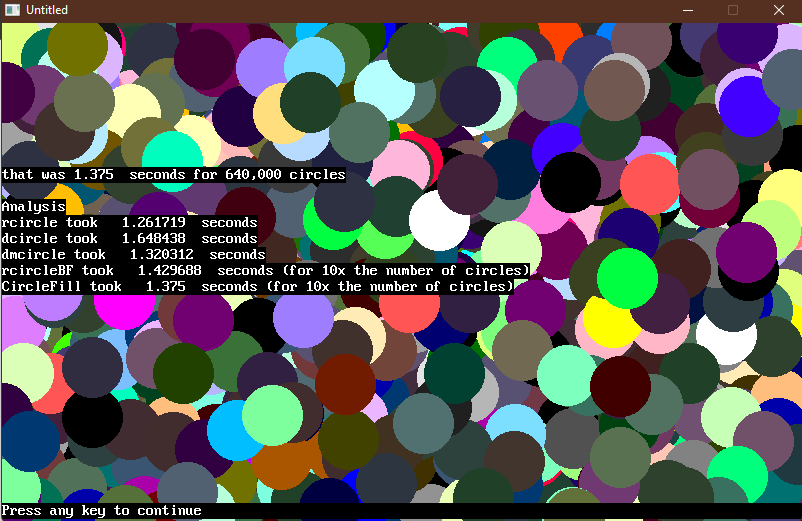
Note that since the last two are running so fast, I upped them to making and filling 640,000 circles instead of 64,000, so the speed difference would be a little more noticeable between the two (and it's not all that different at all!)

[SMcNeill]

Wow BF makes that much a difference? Seems like something is wrong about Line?

BF is highly optimized and is *much* faster than line, just as DO is faster than FOR...

A FOR loop has to track Start, Stop, Step, counting up or down...   A DO loop is just DO.. LOOP and the user has to deal with the exit conditions.  There's a lot less code to process for a DO-LOOP than there is a FOR-Next...

Same way with a line vs a line, BF.   A line has slope.  You calculate rise/run, do a loop, plot the necessary pixels, increment to the next pixel...

BF is just:
FOR y = start to stop
   memfill x, x.start, s.stop, kolor
NEXT

Care to guess which is going to be faster, once you think about the basic premise behind them?  

BF is always quite a bit faster than without it.