Challenges

[bplus]

and the code i used for the solution was

Code: (Select All)

_Title "Sums of consecutive numbers"
' find the numbers between 1 and 1000 that can not be expressed as a sum of a consecutive number.

' ie the sum of 2 consecutives is 2n + 1 from n + (n + 1)
'    the sum of 3                 3n + 3 from n + (n + 1) + (n + 2)
'    the sum of 4                 4n + 6 from n + (n + 1) + (n + 2) + (n + 3)
'    the sum of 5                 5n + 10  from n + (n + 1) + (n + 2) + (n + 3) + (n + 4)
' ...
'    the sum of m consecutives is m*n + m*(m - 1)/2
$Console:Only
Width 140
Dim numbers(1 To 1000) As Integer
m = 2
n = 1
While m < 50
    x = m * n + m * (m - 1) / 2
    While x < 1001
        'Print m, n, x, "zzz..."
        'Sleep
        numbers(x) = numbers(x) + 1
        n = n + 1
        x = m * n + m * (m - 1) / 2
    Wend
    m = m + 1
    n = 1
Wend
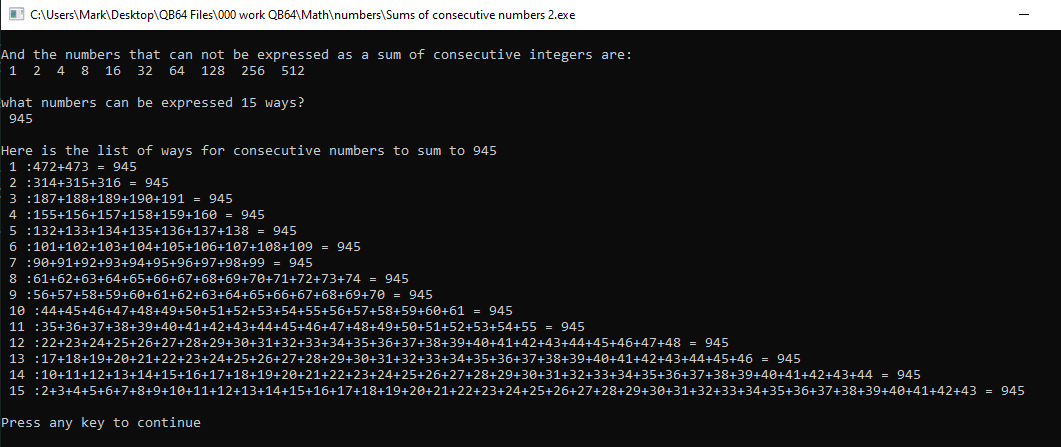
Print: Print "And the numbers that can not be expressed as a sum of consecutive integers are:"
top = 1
For i = 1 To 1000
    If numbers(i) > top Then top = numbers(i)
    If numbers(i) = 0 Then Print i;
Next

' !!! result ONLY powers of 2 can not be a sum of consecutive numbers !!!
Print: Print: Print "what numbers can be expressed"; top; "ways?"
For i = 1 To 1000
    If numbers(i) = top Then save = i: Print i,
Next

' !!! result 945 is expressed 15 different ways !!!

Print: Print: Print "Here is the list of ways for consecutive numbers to sum to"; save
consecSets (save)

Sub consecSets (n)
    For i = 2 To 50
        o = n - i * (i - 1) / 2
        If o Mod i = 0 And o > 0 Then
            count = count + 1
            j = o \ i
            Print count; ":"; ts$(j); "+";
            tot = j
            For k = 1 To i - 1
                tot = tot + j + k
                If k = i - 1 Then Print ts$(j + k); " = "; ts$(tot) Else Print ts$(j + k); "+";
            Next
        End If
    Next
End Sub

Function ts$ (n)
    ts$ = _Trim$(Str$(n))
End Function