I was playing around with the paddle that you can angle with Mouse Wheel and thought it might be fun to do a Pongy style game with it like Ken's, so here it is!
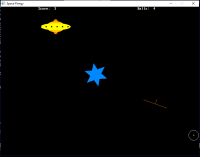
Use mouse wheel to angle paddle either to bounce ball into Spaceship Or keep ball away from the Death Star.
You score a point when ball hits towards center of ship and lose a ball if Death Star runs into ball. You get 5 balls per game.
Life is short in space.
Use mouse wheel to angle paddle either to bounce ball into Spaceship Or keep ball away from the Death Star.
You score a point when ball hits towards center of ship and lose a ball if Death Star runs into ball. You get 5 balls per game.
Code: (Select All)
_Title "Space Pongy" 'b+ started 2020-03-08 from _vince idea Angle Paddle Collision
' 2024-11-29 Make game in style of Ken's Pongy
Const xmax = 800, ymax = 600, xc = 400, yc = 300
Dim Shared P, P2, Pd2
P = _Pi: P2 = 2 * P: Pd2 = P / 2
Dim Shared sx, sy, srI, srO, snP, sa, sdx, sdy ' death Star
Screen _NewImage(xmax, ymax, 32)
_ScreenMove 280, 60
Randomize Timer
bx = xc: by = yc: br = 20: bs = 5: ba = _D2R(60): ball = 5
mr = 50: ma = 0
goalx = 325: goaly = 80
goaldir = 2
NewStar
While _KeyDown(27) = 0
Cls
drawShip goalx, goaly, 2, &HFFFFFF00
goalx = goalx + goaldir
If goalx > 700 And goaldir = 2 Then goaldir = -2
If goalx < 100 And goaldir = -2 Then goaldir = 2
If _Hypot(bx - goalx, by - goaly) < br + 40 Then
score = score + 1: bx = _Width - goalx: by = _Height - goaly: ba = _Pi(2) * Rnd
For snd = 300 To 900 Step 50
Sound snd, .5
Next snd
End If
Circle (bx, by), br 'ball
Circle (bx, by), 2, &HFFFFFF00 'ball
drawStar
Locate 1, 20: Print "Score: "; score
Locate 1, 70: Print "Balls: "; ball
bdx = bs * Cos(ba): bdy = bs * Sin(ba)
bx = bx + bdx
If bx < br Then bx = br: bdx = -bdx
If bx > xmax - br Then bx = xmax - br: bdx = -bdx
by = by + bdy
If by < br Then by = br: bdy = -bdy
If by > ymax - br Then by = ymax - br: bdy = -bdy
ba = _Atan2(bdy, bdx)
While _MouseInput ' paddle
ma = ma + _MouseWheel * P2 / 72 '5 degrees change
Wend
mx = _MouseX: my = _MouseY
mx1 = mx + mr * Cos(ma)
my1 = my + mr * Sin(ma)
mx2 = mx + mr * Cos(ma + P)
my2 = my + mr * Sin(ma + P)
Line (mx1, my1)-(mx2, my2), &HFFFF8800
'draw a handle to track the side the ball is on
hx1 = mx + br * Cos(ma + Pd2): hy1 = my + br * Sin(ma + Pd2)
hx2 = mx + br * Cos(ma - Pd2): hy2 = my + br * Sin(ma - Pd2)
d1 = _Hypot(hx1 - bx, hy1 - by): d2 = _Hypot(hx2 - bx, hy2 - by)
If d1 < d2 Then
Line (hx2, hy2)-(mx, my), &HFFFF8800
paddleNormal = _Atan2(my - hy2, mx - hx2)
Else
Line (hx1, hy1)-(mx, my), &HFFFF8800
paddleNormal = _Atan2(my - hy1, mx - hx1)
End If
tx = -99: ty = -99
dist = _Hypot(bx - mx, by - my) ' collision?
If dist < br + mr Then ' centers close enough
contacts = lineIntersectCircle%(mx1, my1, mx2, my2, bx, by, br, ix1, iy1, ix2, iy2)
'If contacts Then Print "Contact"; contacts ': _DELAY .5 'OK so far
If contacts = 1 Then 'just touched (or passed through)
If _Hypot(ix1 - mx, iy1 - my) < br Then tx = ix1: ty = iy1
ElseIf contacts = 2 Then
'contact point would have been in middle of 2 points
tx = (ix1 + ix2) / 2: ty = (iy1 + iy2) / 2
End If
If tx > 0 Then ' rebound ball
Circle (tx, ty), 2 'show contact point
'relocate bx, by
bx = tx + br * Cos(paddleNormal) 'this is where the ball would be at contact
by = ty + br * Sin(paddleNormal)
'find the angle of reflection
ba = _Atan2(bdy, bdx)
aReflect = Abs(paddleNormal - ba) 'apparently I have to flip the next clac by PI
If ba < paddleNormal Then ba = paddleNormal + aReflect + P Else ba = paddleNormal - aReflect + P
End If
End If
'update death Star
sx = sx + sdx
If sx < srO Then sx = srO: sdx = -sdx
If sx > xmax - sor Then sx = xmax - sr0: sdx = -sdx
sy = sy + sdy
If sy < srO Then sy = srO: sdy = -sdy
If sy > ymax - srO Then sy = ymax - srO: sdy = -sdy
sa = sa + _Pi * .05
If _Hypot(sx - bx, sy - by) < br + srO Then
ball = ball - 1
For snd = 1200 To 200 Step -50
Sound snd, .5
Next
If ball <= 0 Then ' game over
Sleep
End
End If
NewStar
End If
'If _Hypot(goalx - sx, goaly - sy) < 40 + srO Then
' For snd = 900 To 300 Step -50
' Sound snd, .5
' Next
' NewStar
' bx = _Width - goalx: by = _Height - goaly: ba = _Pi(2) * Rnd
'End If
_Display
_Limit 60
Wend
' return 0 no Intersect, 1 = tangent 1 point touch, 2 = 2 point intersect
Function lineIntersectCircle% (lx1, ly1, lx2, ly2, cx, cy, r, ix1, iy1, ix2, iy2)
'needs SUB slopeYintersect (X1, Y1, X2, Y2, slope, Yintercept)
If lx1 <> lx2 Then
slopeYintersect lx1, ly1, lx2, ly2, m, Y0 ' Y0 otherwise know as y Intersect
' https://math.stackexchange.com/questions/228841/how-do-i-calculate-the-intersections-of-a-straight-line-and-a-circle
A = m ^ 2 + 1
B = 2 * (m * Y0 - m * cy - cx)
C = cy ^ 2 - r ^ 2 + cx ^ 2 - 2 * Y0 * cy + Y0 ^ 2
D = B ^ 2 - 4 * A * C 'telling part of Quadratic formula = 0 then circle is tangent or > 0 then 2 intersect points
If D < 0 Then ' no intersection
ix1 = -999: iy1 = -999: ix2 = -999: iy2 = -999: lineIntersectCircle% = 0
ElseIf D = 0 Then ' one point tangent
x1 = (-B + Sqr(D)) / (2 * A)
y1 = m * x1 + Y0
ix1 = x1: iy1 = y1: ix2 = -999: iy2 = -999: lineIntersectCircle% = 1
Else '2 points
x1 = (-B + Sqr(D)) / (2 * A): y1 = m * x1 + Y0
x2 = (-B - Sqr(D)) / (2 * A): y2 = m * x2 + Y0
ix1 = x1: iy1 = y1: ix2 = x2: iy2 = y2: lineIntersectCircle% = 2
End If
Else 'vertical line
If r = Abs(lx1 - cx) Then ' tangent
ix1 = lx1: iy1 = cy: ix2 = -999: iy2 = -999: lineIntersectCircle% = 1
ElseIf r < Abs(lx1 - cx) Then 'no intersect
ix1 = -999: iy1 = -999: ix2 = -999: iy2 = -999: lineIntersectCircle% = 0
Else '2 point intersect
ydist = Sqr(r ^ 2 - (lx1 - cx) ^ 2)
ix1 = lx1: iy1 = cy + ydist: ix2 = lx1: iy2 = cy - ydist: lineIntersectCircle% = 2
End If
End If
End Function
Sub slopeYintersect (X1, Y1, X2, Y2, slope, Yintercept) ' fix for when x1 = x2
slope = (Y2 - Y1) / (X2 - X1)
Yintercept = slope * (0 - X1) + Y1
End Sub
Sub drawShip (x, y, scale, colr As _Unsigned Long) 'shipType collisions same as circle x, y radius = 30
Static ls
Dim light As Long, r As Long, g As Long, b As Long
r = _Red32(colr): g = _Green32(colr): b = _Blue32(colr)
fellipse x, y, 6 * scale, 15 * scale, _RGB32(r, g - 120, b - 100)
fellipse x, y, 18 * scale, 11 * scale, _RGB32(r, g - 60, b - 50)
fellipse x, y, 30 * scale, 7 * scale, _RGB32(r, g, b)
For light = 0 To 5
fcirc x - 30 * scale + scale * 11 * light + ls * scale, y, 1 * scale, _RGB32(ls * 50, ls * 50, ls * 50)
Next
ls = ls + 1
If ls > 5 Then ls = 0
End Sub
' ======== helper subs for drawShip that you can use for other things specially fcirc = fill_circle x, y, radius, color
Sub fellipse (CX As Long, CY As Long, xr As Long, yr As Long, C As _Unsigned Long)
If xr = 0 Or yr = 0 Then Exit Sub
Dim h2 As _Integer64, w2 As _Integer64, h2w2 As _Integer64
Dim x As Long, y As Long
w2 = xr * xr: h2 = yr * yr: h2w2 = h2 * w2
Line (CX - xr, CY)-(CX + xr, CY), C, BF
Do While y < yr
y = y + 1
x = Sqr((h2w2 - y * y * w2) \ h2)
Line (CX - x, CY + y)-(CX + x, CY + y), C, BF
Line (CX - x, CY - y)-(CX + x, CY - y), C, BF
Loop
End Sub
Sub fcirc (x As Long, y As Long, R As Long, C As _Unsigned Long) 'vince version fill circle x, y, radius, color
Dim x0 As Long, y0 As Long, e As Long
x0 = R: y0 = 0: e = 0
Do While y0 < x0
If e <= 0 Then
y0 = y0 + 1
Line (x - x0, y + y0)-(x + x0, y + y0), C, BF
Line (x - x0, y - y0)-(x + x0, y - y0), C, BF
e = e + 2 * y0
Else
Line (x - y0, y - x0)-(x + y0, y - x0), C, BF
Line (x - y0, y + x0)-(x + y0, y + x0), C, BF
x0 = x0 - 1: e = e - 2 * x0
End If
Loop
Line (x - R, y)-(x + R, y), C, BF
End Sub
Sub NewStar
r = Rnd * 5 + 1
sx = Rnd * _Width: sy = Rnd * _Height: srI = Rnd * 20 + 10: srO = Rnd * 20 + 5 + 30
snP = Int(Rnd * 7) + 3: sa = _Pi(2 * Rnd): sdx = r * Cos(sa): sdy = r * Sin(sa)
End Sub
Sub drawStar
star sx, sy, srI, srO, snP, sa, &HFF0088FF
End Sub
Sub star (x, y, rInner, rOuter, nPoints, angleOffset, K As _Unsigned Long)
' x, y are same as for circle,
' rInner is center circle radius
' rOuter is the outer most point of star
' nPoints is the number of points,
' angleOffset = angle offset IN DEGREES, it will be converted to radians in sub
' this is to allow us to spin the polygon of n sides
Dim pAngle, radAngleOffset, x1, y1, x2, y2, x3, y3, i As Long
pAngle = _D2R(360 / nPoints): radAngleOffset = _D2R(angleOffset)
x1 = x + rInner * Cos(radAngleOffset)
y1 = y + rInner * Sin(radAngleOffset)
For i = 0 To nPoints - 1
x2 = x + rOuter * Cos(i * pAngle + radAngleOffset + .5 * pAngle)
y2 = y + rOuter * Sin(i * pAngle + radAngleOffset + .5 * pAngle)
x3 = x + rInner * Cos((i + 1) * pAngle + radAngleOffset)
y3 = y + rInner * Sin((i + 1) * pAngle + radAngleOffset)
ftri x1, y1, x2, y2, x3, y3, K
'triangles leaked
Line (x1, y1)-(x2, y2), K
Line (x2, y2)-(x3, y3), K
Line (x3, y3)-(x1, y1), K
x1 = x3: y1 = y3
Next
Paint (x, y), K, K
End Sub
Sub ftri (x1, y1, x2, y2, x3, y3, K As _Unsigned Long)
Dim D As Long
Static a&
D = _Dest
If a& = 0 Then a& = _NewImage(1, 1, 32)
_Dest a&
_DontBlend a& ' '<<<< new 2019-12-16 fix
PSet (0, 0), K
_Blend a& '<<<< new 2019-12-16 fix
_Dest D
_MapTriangle _Seamless(0, 0)-(0, 0)-(0, 0), a& To(x1, y1)-(x2, y2)-(x3, y3)
End SubLife is short in space.

724 855 599 923 575 468 400 206 147 564 878 823 652 556 bxor cross forever





