Everything in Degrees instead of Radians

[bplus]

Would it make understanding graphics easier to follow, specially employing Sin, Cos and _Atan2?

Here I've converted Sin, Cos, _Atan2, DrawArc and ArrowTo to using Degree Units in the Call to the Sub and internalized all the radian conversions inside the Sub.

Here is main Demo:

Code: (Select All)

' OK let's be rid on the confusion caused by Radians
' by using User Defined Functions SinD and CosD that take Degrees 0 to 360 for whole circle,
' and having replaced _Atan2 by returning an angle in Degrees between 2 points: DAtan2(baseX, baseY, angleToX, angleToY)

_Title "Degrees for everything" 'b+ 2022-10-12
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50

cx = _Width / 2 ' middle of the screen point  center x
cy = _Height / 2 ' center y
radius = 250 ' max is 300 for height 600
ArrowTo cx, cy, 0, radius - 3, &HFFFFFFFF
For degrees = 0 To 359 Step 10 ' go around a full circle in degrees in steps of 10 degrees

    ' calculate and draw points around the center of the screen
    x = cx + radius * CosD(degrees) ' use CosD for x dimensions
    y = cy + radius * SinD(degrees) ' use SinD for y dimensions
    Circle (x, y), 1 ' draw bigger points than single pixel

    ' labeling the degree angles before or after the point ?
    If x < cx Then Xoffset = -10 * Len(_Trim$(Str$(degrees))): YOffset = 0
    If x > cx Then Xoffset = 4 * Len(_Trim$(Str$(degrees))): YOffset = 0
    If x = cx Then
        Xoffset = -4 * Len(_Trim$(Str$(degrees)))
        If y > cy Then YOffset = 20 Else YOffset = -20
    End If
    _PrintString (x + Xoffset, y - 8 + YOffset), _Trim$(Str$(degrees))
Next

' save our compass dial to image
dial& = _NewImage(_Width, _Height, 32)
_PutImage , 0, dial& ' screen to dial image stored

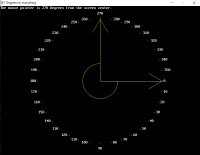
' Getting use to seeing angles mouse makes to center of screen
Do
    Cls
    _PutImage , dial&, 0
    While _MouseInput: Wend ' this checks where mouse is right now!
    mx = _MouseX: my = _MouseY: mb1 = _MouseButton(1) ' left mouse down  ' saves mouse status to common variable names
    'lets's the angle in degrees the mouse is to the center of the screen
    dAngle = DAtan2(cx, cy, mx, my)
    Print "The mouse pointer is "; _Trim$(Str$(dAngle)); " Degrees from the screen center." ' then center point is first the mouse point is second
    ArrowTo cx, cy, dAngle, radius - 3, &HFFFFFF00
    drawArc cx, cy, 70, 0, dAngle, &HFFFFFF00
    _Display ' stop the blinking
    _Limit 60 ' only loop 60 times per second
Loop Until _KeyDown(27)


' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    CosD = Cos(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    SinD = Sin(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2)  makes to a first point (x1, y1)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    ' Delta means change between 1 measure and another for example x2 - x1
    deltaX = x2 - x1
    deltaY = y2 - y1
    '  To find the angle point(x2, y2) makes to (x1, y1) in Degrees
    ' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
    rtn = _R2D(_Atan2(deltaY, deltaX))
    If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function

' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
    Dim As Long x1, y1, x2, y2, x3, y3
    Dim As Double rAngle
    rAngle = _D2R(dAngle)
    x1 = BaseX + lngth * Cos(rAngle)
    y1 = BaseY + lngth * Sin(rAngle)
    x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
    y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
    x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
    y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
    Line (BaseX, BaseY)-(x1, y1), colr
    Line (x1, y1)-(x2, y2), colr
    Line (x1, y1)-(x3, y3), colr
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
    ' xc, yc Center for arc circle
    ' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
    ' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
    ' Arc will start at rStart and go clockwise around for rMeasure Radians

    Dim rStart, rMeasure, rEnd, stepper, a, x, y
    rStart = _D2R(dStart)
    rMeasure = _D2R(dMeasure)
    rEnd = rStart + rMeasure
    stepper = 1 / radius ' the bigger the radius the smaller  the steps
    For a = rStart To rEnd Step stepper
        x = xc + radius * Cos(a)
        y = yc + radius * Sin(a)
        If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
    Next
End Sub

   

[Pete]

Took you long enough. I thought we decide this app needed to be finished before 360 o'clock!

Pete

[bplus]

Hey there's a thought, do everything in o'clock units, AKA Minutes   ... wait that's what we are doing with degrees. OK

Here is introduction to Regular Polygons about the center of the screen. You might think of Regular polygons as pie slices with straight line edges instead of curve. We'll skip the cuts from the center and just straighten up the edges according to number of slices or points on the outer edge.

Code: (Select All)

Option _Explicit
_Title "Degrees for Regular Polygon" 'b+ 2022-10-12
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50
Dim cx, cy, radius, degrees, x, y, xOffset, yOffset, dial&, dStart, NPoints, secDegrees, p, saveX, saveY
cx = _Width / 2 ' middle of the screen point  center x
cy = _Height / 2 ' center y
radius = 250 ' max is 300 for height 600
ArrowTo cx, cy, 0, radius - 3, &HFFFFFFFF
For degrees = 0 To 359 Step 10 ' go around a full circle in degrees in steps of 10 degrees

    ' calculate and draw points around the center of the screen
    x = cx + radius * CosD(degrees) ' use CosD for x dimensions
    y = cy + radius * SinD(degrees) ' use SinD for y dimensions
    Circle (x, y), 1 ' draw bigger points than single pixel

    ' labeling the degree angles before or after the point ?
    If x < cx Then xOffset = -10 * Len(_Trim$(Str$(degrees))): yOffset = 0
    If x > cx Then xOffset = 4 * Len(_Trim$(Str$(degrees))): yOffset = 0
    If x = cx Then
        xOffset = -4 * Len(_Trim$(Str$(degrees)))
        If y > cy Then yOffset = 20 Else yOffset = -20
    End If
    _PrintString (x + xOffset, y - 8 + yOffset), _Trim$(Str$(degrees))
Next

' save our compass dial to image
dial& = _NewImage(_Width, _Height, 32)
_PutImage , 0, dial& ' screen to dial image stored

' A look at Regular Polygons about the Center of the Screen,
' say they all should start at 270 Degrees so they all point North
dStart = 270
For NPoints = 3 To 12
    secDegrees = 360 / NPoints ' how many degree is each section of poly eg triangle = 120 degree
    Cls
    _PutImage , dial&, 0
    For p = 1 To NPoints
        x = cx + radius * CosD(dStart + p * secDegrees)
        y = cy + radius * SinD(dStart + p * secDegrees)
        If p = 1 Then PSet (x, y), &HFFFFFF00: saveX = x: saveY = y Else Line -(x, y), &HFFFFFF00
    Next
    Line -(saveX, saveY), &HFFFFFF00 ' back to first point
    Print "N points ="; NPoints; "  Section angle ="; secDegrees; " degrees,   zzz... press any for next polygon or end..."
    _Display ' stop the blinking
    Sleep '             .
Next

' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    CosD = Cos(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    SinD = Sin(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2)  makes to a first point (x1, y1)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    ' Delta means change between 1 measure and another for example x2 - x1
    Dim deltaX, deltaY, rtn
    deltaX = x2 - x1
    deltaY = y2 - y1
    '  To find the angle point(x2, y2) makes to (x1, y1) in Degrees
    ' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
    rtn = _R2D(_Atan2(deltaY, deltaX))
    If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function

' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
    Dim As Long x1, y1, x2, y2, x3, y3
    Dim As Double rAngle
    rAngle = _D2R(dAngle)
    x1 = BaseX + lngth * Cos(rAngle)
    y1 = BaseY + lngth * Sin(rAngle)
    x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
    y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
    x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
    y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
    Line (BaseX, BaseY)-(x1, y1), colr
    Line (x1, y1)-(x2, y2), colr
    Line (x1, y1)-(x3, y3), colr
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
    ' xc, yc Center for arc circle
    ' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
    ' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
    ' Arc will start at rStart and go clockwise around for rMeasure Radians

    Dim rStart, rMeasure, rEnd, stepper, a, x, y
    rStart = _D2R(dStart)
    rMeasure = _D2R(dMeasure)
    rEnd = rStart + rMeasure
    stepper = 1 / radius ' the bigger the radius the smaller  the steps
    For a = rStart To rEnd Step stepper
        x = xc + radius * Cos(a)
        y = yc + radius * Sin(a)
        If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
    Next
End Sub

[bplus]

OK let's just slip that main code into a Sub and generalize to draw a Regular Polygon about any point x, y with given radius, dStart is where you want to start the polygon st it points out for sure at that angle, for instance we will want allot of Regular Polygons to point due North like 12 o'clock on clock so set dStart to 270 degrees. When testing any alpha color you will see a brighter point where the end line overlaps with the start line. We can do polyFills later where that won't occur.

Code: (Select All)

Option _Explicit
_Title "Sub for Regular Polygon Using Degrees" 'b+ 2022-10-12
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50
Dim i

' Give polygon sub a random workout
Do
    Cls
    For i = 1 To 50
        RegularPoly Rnd * _Width, Rnd * _Height, Rnd * 100 + 5, Int(Rnd * 10) + 3, Rnd * 360, _RGB32(225 * Rnd + 30, 255 * Rnd, 255 * Rnd, 225 * Rnd + 30)
    Next
    Sleep
Loop Until _KeyDown(27)

Sub RegularPoly (cx, cy, radius, nPoints, dStart, K As _Unsigned Long)
    Dim secDegrees, p, x, y, saveX, saveY
    secDegrees = 360 / nPoints
    For p = 1 To nPoints
        x = cx + radius * CosD(dStart + p * secDegrees)
        y = cy + radius * SinD(dStart + p * secDegrees)
        If p = 1 Then PSet (x, y), K: saveX = x: saveY = y Else Line -(x, y), K
    Next
    Line -(saveX, saveY), K ' back to first point
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    CosD = Cos(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    SinD = Sin(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2)  makes to a first point (x1, y1)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    ' Delta means change between 1 measure and another for example x2 - x1
    Dim deltaX, deltaY, rtn
    deltaX = x2 - x1
    deltaY = y2 - y1
    '  To find the angle point(x2, y2) makes to (x1, y1) in Degrees
    ' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
    rtn = _R2D(_Atan2(deltaY, deltaX))
    If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function

' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
    Dim As Long x1, y1, x2, y2, x3, y3
    Dim As Double rAngle
    rAngle = _D2R(dAngle)
    x1 = BaseX + lngth * Cos(rAngle)
    y1 = BaseY + lngth * Sin(rAngle)
    x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
    y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
    x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
    y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
    Line (BaseX, BaseY)-(x1, y1), colr
    Line (x1, y1)-(x2, y2), colr
    Line (x1, y1)-(x3, y3), colr
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
    ' xc, yc Center for arc circle
    ' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
    ' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
    ' Arc will start at rStart and go clockwise around for rMeasure Radians

    Dim rStart, rMeasure, rEnd, stepper, a, x, y
    rStart = _D2R(dStart)
    rMeasure = _D2R(dMeasure)
    rEnd = rStart + rMeasure
    stepper = 1 / radius ' the bigger the radius the smaller  the steps
    For a = rStart To rEnd Step stepper
        x = xc + radius * Cos(a)
        y = yc + radius * Sin(a)
        If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
    Next
End Sub

Correction(2022-10-15): I forgot to change the color of the first point from yellow to K, now corrected.

[bplus]

As promised Regular Polygons Filled without any Alpha color problems PLUS the TriFill is a Drawing Utility worth the price of admission in itself!!!

First we draw random sets or Regular Polys Filled, use any key for another set, and escape to see the Spin Demo use x to quit that.

Code: (Select All)

Option _Explicit
_Title "Sub for Regular Polygon Fill Using Degrees" 'b+ 2022-10-13
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50
Dim i

' Give RegularPolygonFill sub a random workout
Do
    Cls
    For i = 1 To 50
        RegularPolyFill Rnd * _Width, Rnd * _Height, Rnd * 100 + 5, Int(Rnd * 10) + 3, Rnd * 360, _RGB32(225 * Rnd + 30, 255 * Rnd, 255 * Rnd, 225 * Rnd + 30)
    Next
    Print "zzz... Esc for next demo, any other for another Random set."
    Sleep
Loop Until _KeyDown(27)

'lets take a set for a spin, User Defined Type (UDT) some poly's
Type poly
    As Single x, y, r, p, dStart, rDir, deltaD, s
    As _Unsigned Long k
End Type

Dim pf(1 To 100) As poly ' poly array to load
For i = 1 To 100 '                             makeup a bunch of poly data
    pf(i).x = Rnd * _Width
    pf(i).y = Rnd * _Height
    pf(i).r = Rnd * 100 + 5 '                              radius
    pf(i).p = Int(Rnd * 10) + 3 '                          n points
    pf(i).dStart = Rnd * 360 '                             start angle of polygon
    If Rnd < .5 Then pf(i).rDir = -1 Else pf(i).rDir = 1 ' direction to spin
    pf(i).deltaD = Rnd * 10 + .5 '                         spin amount
    pf(i).k = _RGB32(225 * Rnd + 30, 255 * Rnd, 255 * Rnd, 225 * Rnd + 30) ' Kolor
Next

Do
    Cls
    For i = 1 To 100
        RegularPolyFill pf(i).x, pf(i).y, pf(i).r, pf(i).p, pf(i).dStart, pf(i).k
        pf(i).dStart = pf(i).dStart + pf(i).rDir * pf(i).deltaD
    Next
    Print "Use x to quit..."
    _Display ' stops blinking
    _Limit 30 ' loop at most 30 times a sec
Loop Until _KeyDown(Asc("x"))

Sub RegularPolyFill (cx, cy, radius, nPoints, dStart, K As _Unsigned Long)
    Dim secDegrees, p, x, y, lastX, lastY, startX, startY
    secDegrees = 360 / nPoints
    For p = 1 To nPoints
        x = cx + radius * CosD(dStart + p * secDegrees)
        y = cy + radius * SinD(dStart + p * secDegrees)
        If p > 1 Then
            TriFill cx, cy, lastX, lastY, x, y, K
        Else
            startX = x: startY = y
        End If
        lastX = x: lastY = y
    Next
    TriFill cx, cy, lastX, lastY, startX, startY, K ' back to first point
End Sub

Sub RegularPoly (cx, cy, radius, nPoints, dStart, K As _Unsigned Long)
    Dim secDegrees, p, x, y, saveX, saveY
    secDegrees = 360 / nPoints
    For p = 1 To nPoints
        x = cx + radius * CosD(dStart + p * secDegrees)
        y = cy + radius * SinD(dStart + p * secDegrees)
        If p = 1 Then PSet (x, y), K: saveX = x: saveY = y Else Line -(x, y), K
    Next
    Line -(saveX, saveY), K ' back to first point
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    CosD = Cos(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    SinD = Sin(_D2R(degrees))
End Function

' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2)  makes to a first point (x1, y1)
    ' Note this function uses whatever the default type is, better not be some Integer Type.
    ' Delta means change between 1 measure and another for example x2 - x1
    Dim deltaX, deltaY, rtn
    deltaX = x2 - x1
    deltaY = y2 - y1
    '  To find the angle point(x2, y2) makes to (x1, y1) in Degrees
    ' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
    rtn = _R2D(_Atan2(deltaY, deltaX))
    If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function

' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
    Dim As Long x1, y1, x2, y2, x3, y3
    Dim As Double rAngle
    rAngle = _D2R(dAngle)
    x1 = BaseX + lngth * Cos(rAngle)
    y1 = BaseY + lngth * Sin(rAngle)
    x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
    y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
    x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
    y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
    Line (BaseX, BaseY)-(x1, y1), colr
    Line (x1, y1)-(x2, y2), colr
    Line (x1, y1)-(x3, y3), colr
End Sub

' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
    ' xc, yc Center for arc circle
    ' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
    ' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
    ' Arc will start at rStart and go clockwise around for rMeasure Radians

    Dim rStart, rMeasure, rEnd, stepper, a, x, y
    rStart = _D2R(dStart)
    rMeasure = _D2R(dMeasure)
    rEnd = rStart + rMeasure
    stepper = 1 / radius ' the bigger the radius the smaller  the steps
    For a = rStart To rEnd Step stepper
        x = xc + radius * Cos(a)
        y = yc + radius * Sin(a)
        If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
    Next
End Sub

''   BEST saves dest and optimized with Static a& and alpha colors work better
'2019-12-16 fix by Steve saves some time with STATIC and saves and restores last dest
Sub TriFill (x1, y1, x2, y2, x3, y3, K As _Unsigned Long) ' 2022-10-13 changed name
    Dim D As Long
    Static a&
    D = _Dest
    If a& = 0 Then a& = _NewImage(1, 1, 32)
    _Dest a&
    _DontBlend a& '  '<<<< new 2019-12-16 fix
    PSet (0, 0), K
    _Blend a& '<<<< new 2019-12-16 fix
    _Dest D
    _MapTriangle _Seamless(0, 0)-(0, 0)-(0, 0), a& To(x1, y1)-(x2, y2)-(x3, y3)
End Sub

Correction (2022-10-16): Though not used here, I forgot to change the color of the first point drawn in Sub for drawing regular polygons, fixed now.

[triggered]

What I find funny about this thread is that people who know trigonometry just account for the backwards y-coordinate without incident. On the other hand - People who don't know trigonometry are absolutely not being helped when they see the unit circle being generated upside down, as done here. Bplus, ever heard of WINDOW and why not use it for graphics-heavy programs? Genuine question.

[mnrvovrfc]

Comes from somebody who doesn't speak BASIC as first language. :/

It's a graphics program for visual enjoyment, not to teach trigonometry. It's being done more for fun than to learn how a math function works. The master will teach if he/she wants to do so.

EDIT: Not using "WINDOW" just means scaling (multiplication) and skewing (addition) the results of "SIN()", "TAN()" and other such functions. The "essence" of the sinewave could be demonstrated, and why "TAN()" doesn't produce a good graph LOL without adjusting it a bit.

How many people who "don't know" trigonometry would consider visiting a forum about BASIC programming in the first place?

[bplus]

What I find funny about this thread is that people who know trigonometry just account for the backwards y-coordinate without incident. On the other hand - People who don't know trigonometry are absolutely not being helped when they see the unit circle being generated upside down, as done here. Bplus, ever heard of WINDOW and why not use it for graphics-heavy programs? Genuine question.

I thought you were Stx  but a unit circle has a radius of one, and Stx would know that. Still any one who says the coordinate system is backwards sounds like from that camp.

@triggered are you STx AKA now Sprezzo?

[bplus]

Comes from somebody who doesn't speak BASIC as first language. :/

It's a graphics program for visual enjoyment, not to teach trigonometry. It's being done more for fun than to learn how a math function works. The master will teach if he/she wants to do so.

EDIT: Not using "WINDOW" just means scaling (multiplication) and skewing (addition) the results of "SIN()", "TAN()" and other such functions. The "essence" of the sinewave could be demonstrated, and why "TAN()" doesn't produce a good graph LOL without adjusting it a bit.

How many people who "don't know" trigonometry would consider visiting a forum about BASIC programming in the first place?

Actually I WAS trying to show how to use Trig functions on Basic screen without WINDOW modification because that involves allot of conversions, particularly mouse and that's not worst. Only a few graphics commands adjust to WINDOW conversions, certainly not drawing arcs with CIRCLE.

[James D Jarvis]

Wait a minute.... how are you getting zero degrees to point to the right along the x axis? When I pop 0 degrees into sin and cos I end up with it going along the Y axis.

OH CRUD. Have I been failing to account for the top left corner being 0,0 on the standard screen?

I've been doing:
newX= oldx+range*sin(angle)
newY= oldy+range*cos(angle)

which of couse works but 0 degress points straight "down" the screen along the Y axis.